Why We Should Be Serious About Games

Why we should be serious about games

Quantum game theory introduces fascinating scenarios known as pseudo-telepathy games, where two players can achieve higher success probabilities by using the laws of quantum mechanics rather than classical physics.

More precisely, there exist games with a Perfect Quantum Strategy (PQS), strategies that guarantee a 100% success rate using quantum resources, even though no classical strategy can win with certainty. These quantum games are not just clever thought experiments: they serve as deep tests of quantum properties such as entanglement and contextuality, and they touch on some of the most profound questions in modern physics.

Today, thanks to quantum computers, we can actually play such games from our laptops.

Playing the Mermin Game

Let’s look at one of the simplest examples, the Mermin game.

Two players, Alice and Bob, are not allowed to communicate during the game. A referee, Charlie, sends a question x to Alice and a question y to Bob, where both x and y belong to the set {1,2,3}.

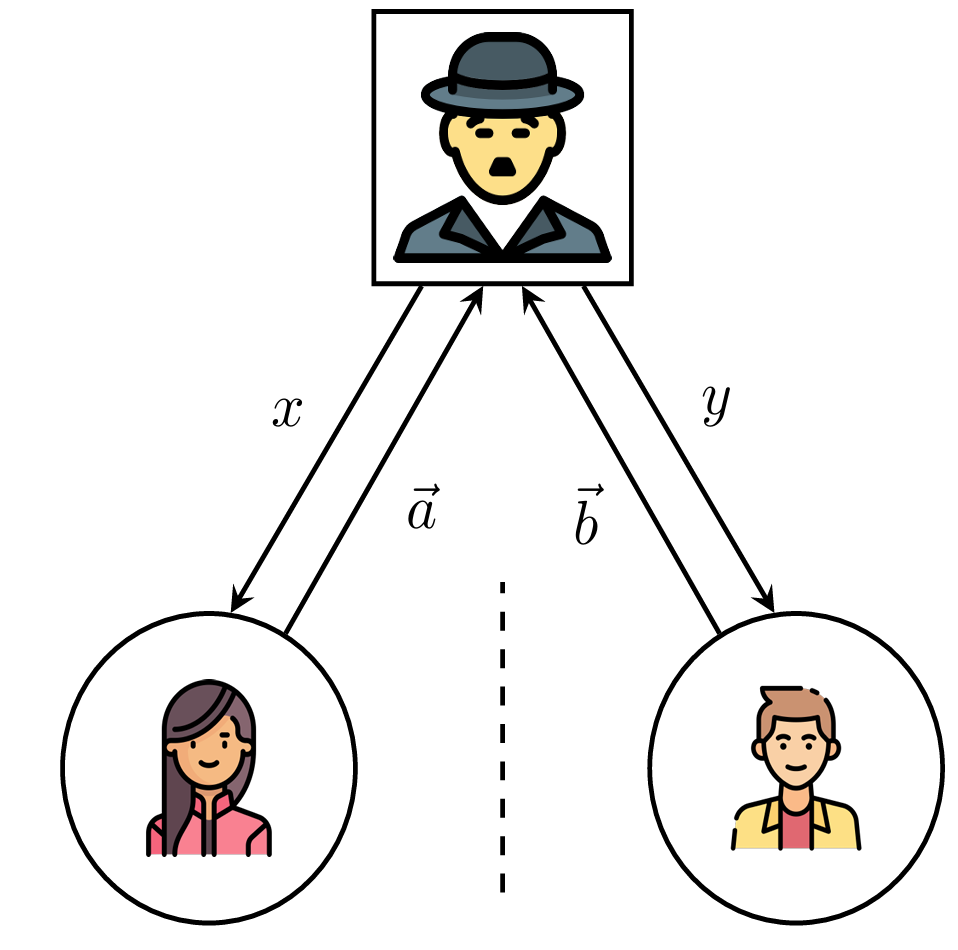
Each player responds with a triplet of numbers:

• Alice sends (a₁ , a₂ ,a₃) ,
• Bob sends (b₁ , b₂ , b₃) ,
• where every element a_i , b_j is either +1 or −1

Their responses must also satisfy these conditions:

• Alice’s triplet must multiply to 1, a₁ ∗ a₂ ∗ a₃ = 1  
• Bob’s triplet must multiply to −1, b₁ ∗ b₂ ∗ b₃ = −1

Alice and Bob win the game if and only if a_y = b_x

‍

Let’s do an example: Suppose Alice receives x = 2 and Bob receives y = 1 . Alice sends (1,−1,−1) which is valid since 1∗(−1)∗(−1)=1. Bob sends (1, 1,−1) which is also valid since 1∗1∗(−1)=−1.

Here, a_y = a₁ = 1 and b_x =b₂ = 1, so they win the game.

Now, if Alice and Bob try to find a classical deterministic strategy that always wins, they quickly run into a paradox. We can represent their strategies as a 3×3 table, where rows correspond to Alice’s answers and columns to Bob’s. The intersection (x, y) must always satisfy a_y = b_x. However, the constraints on the products of rows and columns make it impossible to fill the entire table consistently: the product of each row must be +1 , while the product of each column must be −1. This contradiction means that no classical strategy can guarantee victory, the best they can do is win 8 times out of 9.

But if Alice and Bob share quantum entanglement, they can design a quantum strategy that wins every single round [1].

How Profound Is the Mermin Game?

The Mermin game, originally proposed by Adán Cabello [2], is a classic example of a nonlocal or pseudo-telepathy game. It beautifully illustrates a fundamental quantum phenomenon known as contextuality.

Roughly speaking, quantum contextuality refers to the result of Kochen and Specker [3], who proved that no classical (or “hidden-variable”) model can reproduce all quantum predictions unless it allows measurement outcomes to depend on the measurement context, that is, on which other compatible measurements are performed. This “no-go” theorem shows that quantum outcomes cannot be explained by pre-existing hidden properties independent of context.

Alongside entanglement, contextuality has become a key resource in quantum information science. It underlies several notions of quantum computational advantage [4, 5]. The Mermin game has not only been used to experimentally test contextuality but also appears in some of the most profound theoretical developments, including the proof of Connes’ Embedding Conjecture and the resolution of Tsirelson’s problem [6].

Playing Contextuality Games on a Quantum Computer

Today, thanks to Noisy Intermediate-Scale Quantum (NISQ) computers, the Mermin game can be implemented and tested experimentally.

As part of the TACTICQ¹ project, in which ColibriTD is a partner, Colm Kelleher has developed new pseudo-telepathy game scenarios based on finite geometric configurations and successfully tested them on the latest generation of IBM quantum processing units with remarkable accuracy [7].

In his work, the non-local  games emerge as a bridge connecting geometry, quantum foundations, and practical experimentation on today’s quantum devices. More than just a game, it is a window into the nonclassical nature of reality itself.

References

[1] https://en.wikipedia.org/wiki/Quantum_pseudo-telepathy

[2] Cabello, A. (2001). Bell’s theorem without inequalities and without probabilities for two observers. Phys. Rev. Lett., 86, 1911.

[3] Kochen, S., & Specker, E. P. (1967). The Problem of Hidden Variables in Quantum Mechanics. Journal of Mathematics and Mechanics, 17.

[4] Howard, M., Wallman, J., Veitch, V., & Emerson, J. (2014). Contextuality supplies the “magic” for quantum computation. Nature, 510(7505), 351–355.

[5] Bravyi, S., Gosset, D., König, R., & Tomamichel, M. (2020). Quantum advantage with noisy shallow circuits. Nature Physics, 16(10), 1040–1045.

[6] Ji, Z., Natarajan, A., Vidick, T., Wright, J., & Yuen, H. (2021). MIP = RE*. Communications of the ACM, 64(11), 131–138.

[7] Kelleher, C., & Holweck, F. (2025). Empirical Demonstration of Quantum Contextuality on NISQ Computers. arXiv:2505.21243.

______________________

¹ Techniques Avancées de Calcul pour la Théorie de l’Information et du Contrôle Quantique  supported by ANR-17-EURE0002