Our vision

We aim to cover various use cases, such as material deformation or climate simulations. The workflow of our program can be simply described in the following manner:

The user inputs their problem parameters and meta-parameters. These can determine, for example, the maximum length or budget - or even the minimal precision of the required solution.

The input parameters are then used in our platform to choose an optimal algorithm, computational time as well as the ideal device.

After the initialization of the parameters and meta-parameters, specialized modules are called on our servers. This includes our quantum advantage module. While other modules prepare the data for the optimal algorithm, the quantum advantage module is one that decides the ideal quantum algorithm along with the choice of parameters (e.g., number of iterations, qubits, etc).

The chosen quantum algorithm is run in our abstract language library, and executed on our partner's hardware. Following the execution of the quantum algorithm, our platform interprets the results in a presentable and familiar format for the customer.

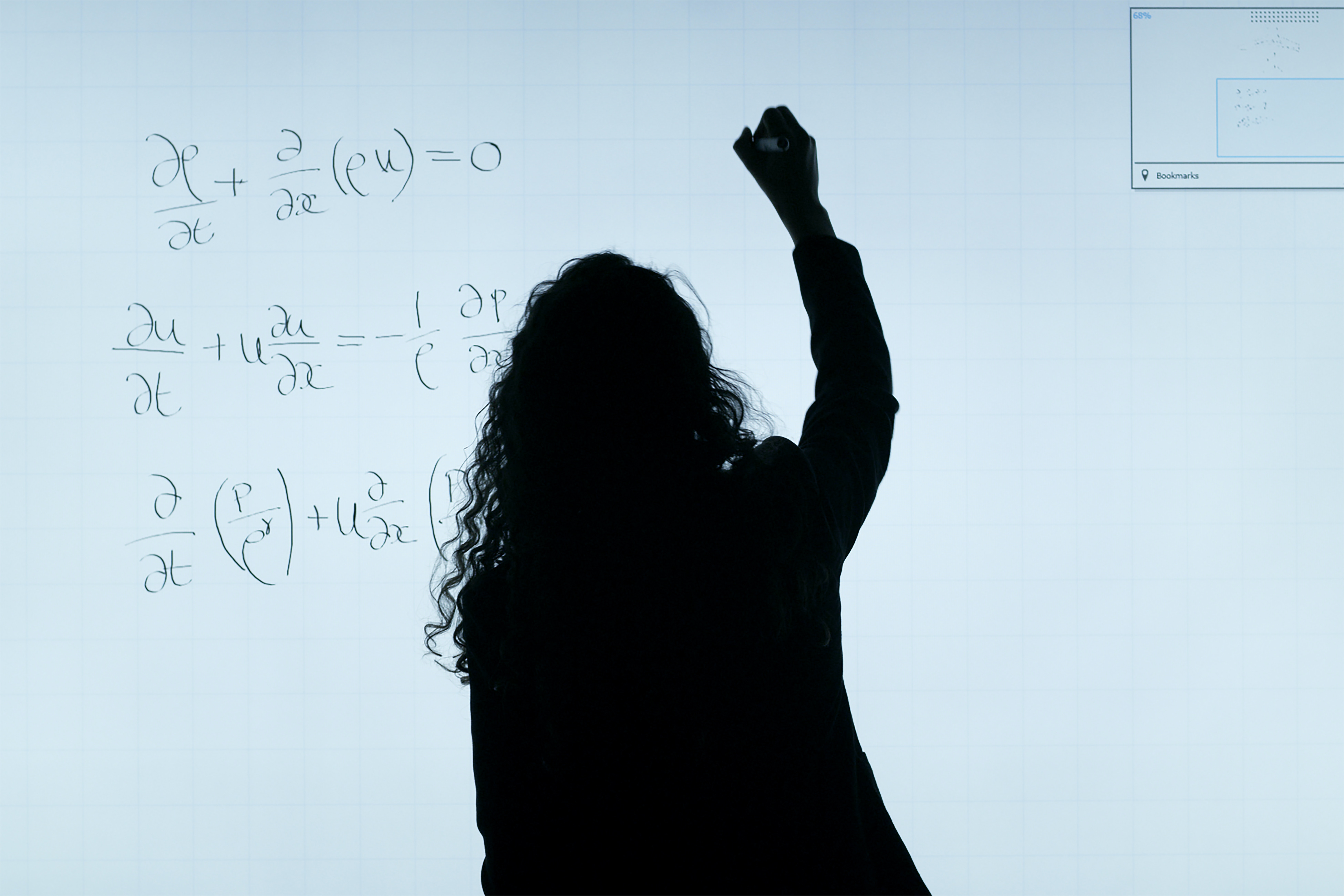
Our future

Our team at ColibriTD is working hard to discover various advantages that quantum technology can provide. The key focus is not only on optimized time consumption, but on solution accuracy as well as energy consumption. We aim to provide environmentally friendly and sustainable solutions for complex problems.

We are here to democratize quantum computing, and provide our customers with advantages brought by quantum technology.

Your use case

Our goal is to bring quantum computing to everyone and make quantum technologies more accessible through our QUICK-platform, as well as our team of quantum researchers. Namely, we would be very excited to tackle any of the following use cases - and much more.If your use case is very different from the ones described below, we would still love to hear from you.
‍

Cases modeled by the Navier–Stokes equations

The Navier–Stokes equations can be used to mathematically model fluid dynamics, climate science, macroeconomics, and has plenty of applications in engineering - thus, they play a crucial role in quantum computing.

It has been shown that quantum computers can bring remarkable advantage when solving linear differential equations. However, quantum solutions do not exist without some challenges - more specifically, here lies the issue: quantum mechanics are linear in nature. This makes nonlinear problems, such as the Navier–Stokes equations, difficult to solve.

However, there are several powerful quantum algorithms that can be implemented in order to efficiently solve partial differential equations (PDEs) on a quantum computer. Our solution can be systematically implemented to various use cases that can be modeled by PDEs - particularly ones modeled by the Navier–Stokes equations.
‍

Fight cancer with quantum solutions

It has been estimated that about 50% of the entire world's population will receive a cancer diagnosis at some point in their lives. Additionally, cancer is currently the second leading cause of death worldwide. To battle this, scientists are continuously working on drug development and various treatment plans - and the process can be made much faster and more efficient by leveraging the power of quantum technology.

Quantum computers can simulate large molecules in precise detail – molecules that are impossible to simulate using a classical computer. This provides a path to safer and more efficient treatment plans.
‍

Optimize your portfolio and get the best return on investment without time-consuming data analysis

A quantum approach can be particularly powerful when finding a company's portfolio which maximizes the return on investment - or one that minimizes risk. This is because quantum computers have been designed to try many possibilities simultaneously in order to find the optimal solution, making them a very powerful tool for these types of tasks.

Moreover, quantum annealers are known to be powerful for optimizing investment portfolios according to the risk margin, allowing for great annual return on investment.
‍

Simulate complex systems in a fraction of the time

Climate modeling and weather forecasting are on the brink of a major quantum-breakthrough, as quantum computers enable researchers to make more accurate predictions with only a fraction of the time when compared to classical computers.

This is not only useful from the perspective of research in environmental and climate sciences, but it offers the potential to transform our battle with climate change by providing fewer technical challenges and a major acceleration of solutions.

The theoretical basis of climate modeling lies in ordinary and partial differential equations. Precisely, the motion of the atmosphere and our oceans can be considered with the application of Navier–Stokes equations, which our platform is designed to tackle.

‍

Model your engineering problem using our quantum platform!

Our platform can be used to tackle various problems in engineering. Namely, QUICK offers quantum solutions that are closely tied to everyday tools used by engineers, which allows them to run top-quality simulations as fast as possible. Examples of such use cases can include, for example, computing various beam deflection scenarios.

With the help of QUICK, the user simply needs to characterize the problem by specifying the material, boundary conditions, and any potential constraints. This is then transferred to QUICK through a script that translates the given problem into the language of partial differential equations. Moreover, thanks to our collaboration with eleQtron, we can provide access to top quantum hardware, including eleQtron, an ion-based quantum computer for appropriate use cases.