Super-conductive qubits
The qubits that power today’s quantum computers come in many different flavours. Superconducting devices, spinning atoms, polarized photons, quantum dots, trapped ions: like a child in an ice cream shop, we can choose the best technology according to our tas… needs! Even within the same technology, qubits can be declined differently. Each qubit type has its advantages and disadvantages and in order to choose the best for our scopes it is key to understand how each kind of qubit is designed and what is the physics behind it. We started this journey toward superconducting ones in my last medium article. This kind of technology is already in use in early-stage NISQ quantum computers made by Google, IBM, and others.
Just to give you a very small recap about the physics behind them (but I strongly recommend you to read the full version of the story), according to B.C.S. theory [1], a superconductive regime is reached for certain materials at critical temperature: once this happens the usually repulsive force between electrons is replaced by a slightly attractive one. As a consequence, the so-called Cooper pairs are formed, and the electrons paired like so are able to flow freely through the superconducting material without scattering, i.e. without an electric resistance.
If you can't see immediately a correlation between superconductivity and quantum computing, don't worry! You are not the first nor probably the last. Indeed, the journey of superconductive qubits from design to realization wasn't that easy. Even though first superconducting qubit experiments went out in 1999 when a team led by physicist Yasunobu Nakamura published a paper [2] demonstrating the first functional superconducting qubit, some in the quantum community spent years arguing that those qubits did not constitute a truly quantum system, forcing superconducting qubits to be little more than a pipe dream for a long time [3].
The reason why this happened is that superconducting qubits are so much larger than other qubits, meaning they technically operate at the macroscopic scale and shouldn't then be ruled by quantum laws typical of microscopic systems. To give you an idea, a superconductive qubit is big enough to be seen with naked eyes!
The first superconductive qubit designed, which is the one we are going to talk about today, was labeled with the name of “charge qubit” and it was the first of many superconducting qubit designs that include flux qubits, and phase qubits [4].
The simplest superconducting qubits
Let’s build together the simplest superconducting circuit, which, ⚠ spoiler alert ⚠, is going to bring us directly to the simplest superconductive qubit.
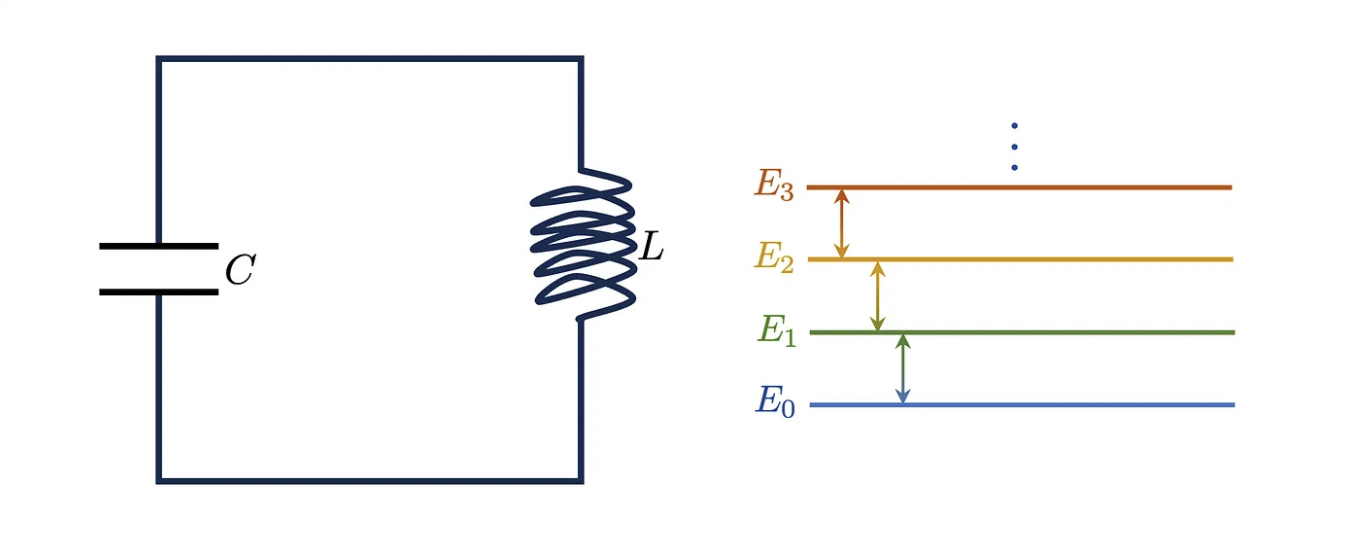
The first thing we have to keep in mind is that it is primordial to preserve the temperature of the circuit: we absolutely don't want it to warm up, otherwise it would go back being a common (and not so great) circuit, losing all its quantum magic. If we want to design such a circuit, we need to use elements that do not produce heat when superconducting. This forces our choice toward capacitors and inductors. The first are used to store energy by means of electric field, the second for the magnetic one. For the sake of simplicity, a capacitor can be imagined as two parallel metallic plates storing electric charge. The main quantity associated with a capacitor is its capacitance C that measures how much charge can be stored in it when connected to a given power source. Concerning the inductors, those are basically wires shaped as a coil and they have the goal to store magnetic fields when a current passes through. The quantity that characterizes an inductor is its inductance 𝐿, which measures the strength of the magnetic field stored in the inductor at a fixed current. Knowing this, the simplest circuit we can build is a capacitor connected to an inductor, this is called LC circuit and is depicted below on the left side [5].

The energy levels of it can be modeled as a quantum harmonic oscillator with quantized energy levels. Unfortunately, we absolutely can't use this circuit as a qubit: the spacing between the energy levels is constant. This brings with it the inconvenience that identical photons would cause energy transitions between many neighbouring pairs of states. This makes it impossible to create a two-level system by isolating just two specific states for our qubit and any attempt to encode a particular state would push the qubit way too far in its energy scale, making it useless for any computation purpose. It seems to be an almost inescapable curse… unless we use a non-linear inductor!
Special guest star: the Josephson junction
What would a non-linear inductance change for our purposes? It would create a non-proportionate change between voltage and current, creating energy level unequally spaced. A direct consequence is the possibility to isolate two out of several energy levels, creating an easy-to-isolate two level system. In a superconductive circuit the element we can use to pursue this goal is the Josephson junction, which acts exactly as a non-linear inductor. The way this is built is very simple, it consists basically of a very thin layer (about a thousandth of a hair thick) of insulating material sandwiched between two aluminum superconducting electrodes (Fig. 2).
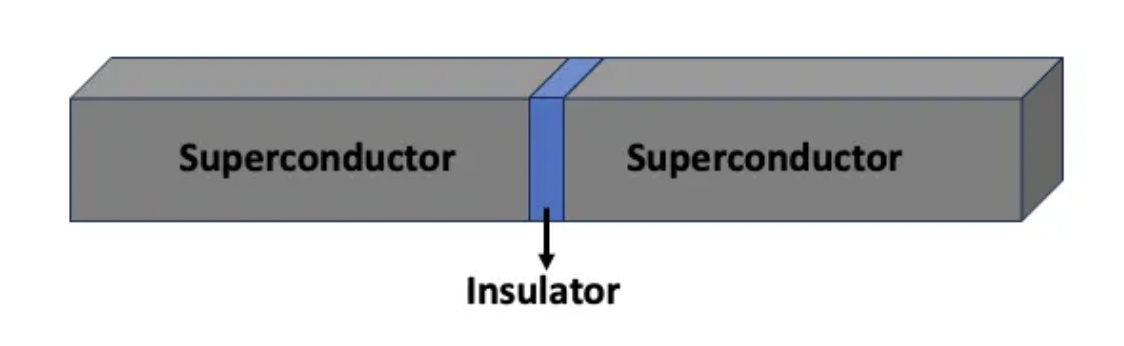
The reason why such an element behaves like a non-linear inductor is hidden in the tunneling effect: it is well-known that Cooper pair can tunnel due to what is called, surprise-surprise, the “Josephson effect”. Named after its discoverer Brian D. Josephson, this effect predicted that pairs of electrons, thanks to their quantum nature, could pass through the structure we mentioned above. This effect represents an example of how a quantum phenomenon can be observed at ordinary instead of the atomic scale: this junction and the quantum nature of Cooper pairs are keeping the current alive even if an insulator is added. Replacing the inductor with this new element labeled as Eⱼ, we obtain unevenly spaced energy levels: the junction provides the non-linearity allowing us to control the states unambiguously (if you want to know more see [6]). We are ready to label as zero the lowest energy level and as one the following one: this a fundamental step in our recipe, since without this ingredient, no superconducting qubits would ever work. It's time to celebrate: congrats, we finally got our artificial atom [4][5]!
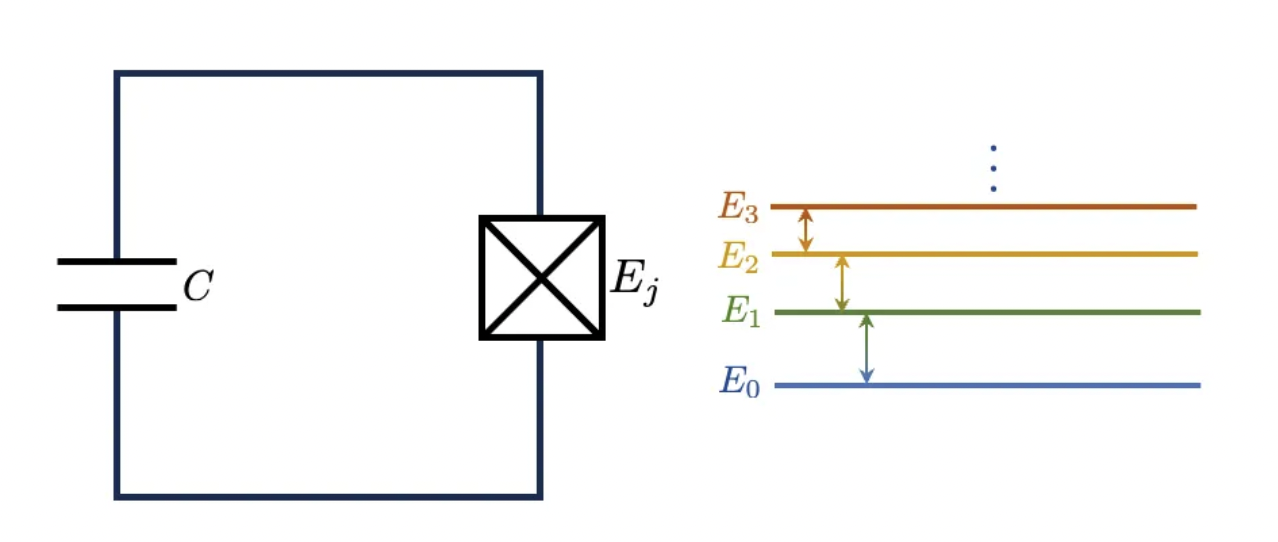
To get a better idea of how a so-built charge qubit works, it useful to think of the circuit as being divided into two regions: following the figure above (Fig. 3), the first region extends from the bottom plate of capacitor C to the Junction Eⱼ, and it is called superconducting “island"; the rest of the circuit including the voltage source is usually addressed as superconducting “reservoir.” In a charge qubit, the zero and one states that form the basis of all quantum computations correspond to the “charge states” of the island region, i.e. the absence or presence of excess Cooper pairs in the island. For this reason, the superconducting island is also known as a “single Cooper-pair box” [4]. By adjusting the voltage it is possible to tune the island putting it in the zero state, in the one state, or a superposition of the two, but about this we are going to be more specific.
We are halfway (or even more) there, but we haven't succeeded yet! So far we only managed to create a two-state system but what we want from that is to build quantum computers. In short, what is missing is the possibility to have a controlled circuit-environment interaction. It's time to add a new element: we want our qubit to be useful in order to build quantum computers and to do so it has to interact with the environment somehow [7].To be more clear, we are going to add a gate capacitor in order to receive external photons (see Fig. 4). The capacitance Cg, can be decided by the constructor and determines how strongly the circuit interacts with the environment.
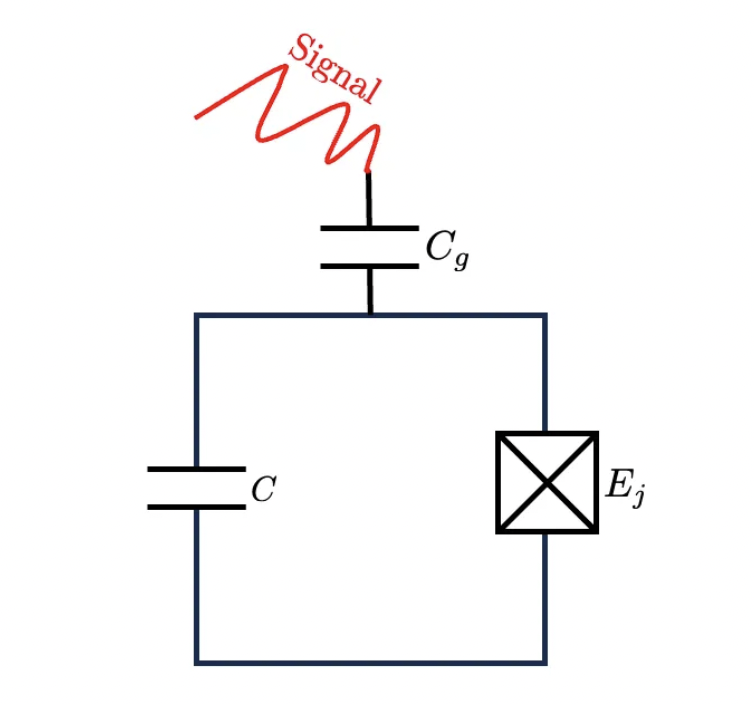
This brand new element adds sadly a brand new problem: since the energy of our levels will depend on Cg as well, we are once again messing up with the unevenly spaced energy levels we fought so hard to get. This is not a big deal actually, we can fix this by changing the other capacitance C, making it larger. This way the energy levels will become less sensitive to the gate capacitance Cg. So, after all, what we need to do is to choose an appropriate capacitor. It is worth mentioning that this solution comes at a cost: this also makes the differences in energy levels more uniform, but, thankfully, the latter problem turns out to be more serious than the former and it turns out to be possible to adjust the capacitance value and preserve the non-uniformity. This regime is known as the transmon regime, and artificial atoms falling in it are called transmons. They are considered among the best superconductive (and not…) qubits and they are exploited correctly from several companies. In the charge qubit, different energy levels correspond to an integer number of Cooper pairs on a superconducting island. Then, to jump from a state to the other, we need to stimulate the transition using photons having energy ℏω equal to the energy gap ΔE standing between the two levels.
Congrats! We managed not only to build a superconductive qubits but also to make it jump from |0⟩ to |1⟩ and viceversa!
But… Before concluding this introduction on superconductive qubits, it is very important to understand how this technology overall ranks according to Di Vincenzo’s criteria [8], which define the five characteristic the ideal qubit technology should have:
1. Well-characterized and scalable, meaning that we must find a way to make the system behave as a qubit and be able to put many of these systems together. In the case of superconductive qubits, we worked very hard in order to obtain a well-characterized two-level system and we succeeded. Concerning the scalability, these qubits still suffer of a problem known as frequency crowding: if we interconnect too many qubits together inside a cavity, they may start to have similar energy gaps! This obstacle can be somehow eluded by changing the connection geometry of the qubit but much more work needs to be done in order to mark this issue as solved.
2. Qubit initialization, meaning we must be able to prepare the same state repeatedly within an acceptable margin of error. What's great about superconductive technology is that this criterion is easily satisfied: being the excited states of an artificial atom unstable, it is sufficient to wait for a short period. A well-isolated system guarantees that all the qubits will be in the ground state with a high probability after this short interval.
3. Ideally qubits should have long coherence times. In order to perform reliable quantum operations, we need qubits that keep their quantum properties as long as possible, even after interacting with their environment. Because of their size, superconducting circuits interact with the environment in a way that is hard to control, giving rise to a very short decay time: the excited state lasts for about 1 μs before decaying back to the ground state.
4. In order to manipulate the qubit state, each technology needs its own universal set of gates, which means we need both single-qubit and two-qubit gates. For superconductive qubits, the main challenge is given by the two-qubits ones. Luckily, there are many option to connect two qubits: we may link them by means of a superconducting wire, or by confining them in same cavity, etc. Nowadays, one of the best way is via capacitative coupling, where two qubits are connected via a wire and a coupling capacitor [10].
5. Last but not least, we need to measure individual qubits to read and exploit the result of a quantum algorithm. This part may be a bit tricky so I'll try to summarize it at best: to extract information, we have to shine light that the superconductive cavity lets through. The photons, running into the qubits, are scattered by them, and the collision will cause an exchange in momentum and energy. Because of that, these photons will store some information about the state of the qubit. As a consequence, if we carefully measure the properties of the scattered light, we can extract information about the state [4].
In conclusion, superconducting qubits are currently considered to be leading candidate for scalable quantum computing. In the last years, thanks to the efforts of the countless big and small companies that rely their technology on them [8], superconductive qubits had an important improvement in coherence time, operation fidelities and qubit readout. Nonetheless, apart from the already mentioned difficulties, superconducting qubits also require dilution refrigerators to maintain temperatures low enough, and also an improvement of this technology should be made before building a device with millions of qubits [11].
At ColibriTD
At ColibriTD we aim at dynamically choosing the best qubit technology for the problem at hand. This requires a deep knowledge of the physics behind each of them in order to design the best algorithm.
References:
[1] J. Bardeen, L.N. Cooper, and J.R. Schrieffer, Theory of Superconductivity, Phys. Rev. 108, 1175 (1957).
[2] Y. Nakamura, Yu. A. Pashkin, J. S. Tsai, Coherent control of macroscopic quantum states in a single-Cooper-pair box, Nature 398, 786 (1999).
[3] R. Alicki, False Qubits?: Polarization of Light and Josephson Junction, OSID14, 223 (2007).
[4] R. Davis, How The First Superconducting Qubit Changed Quantum Computing Forever, Medium (2022).
[5] Alvaro Ballon, Quantum computing with superconducting qubits, Pennylane (2022).
[6] N.F. Pedersen, Non-linear properties of Josephson junctions, Phys. D: Nonlinear Phenomenon 68, 27 (1993).
[7] Jonathan Hu, QC — How to build a Quantum Computer with Superconducting Circuit?, Medium (2019).
[8] D. DiVincenzo, The Physical Implementation of Quantum Computation, Fortschritte der Physik 48, 783, (2000).
[9] J. Dargan, Companies Developing Superconducting Qubits (2023).
[10] J. Cayao, M. Benito, and G. Burkard, Programable two-qubit gates in capacitively coupled flopping-mode spin qubits, Phys. Rev. B 101, 195438 (2020).
[11] A. Blais, A.L. Grimsmo, S. M. Girvin, and A. Wallraff, Circuit quantum electrodynamics, Rev. Mod. Phys. 93, 025005 (2021).





