Quantum computation using ultracold atoms in optical lattices

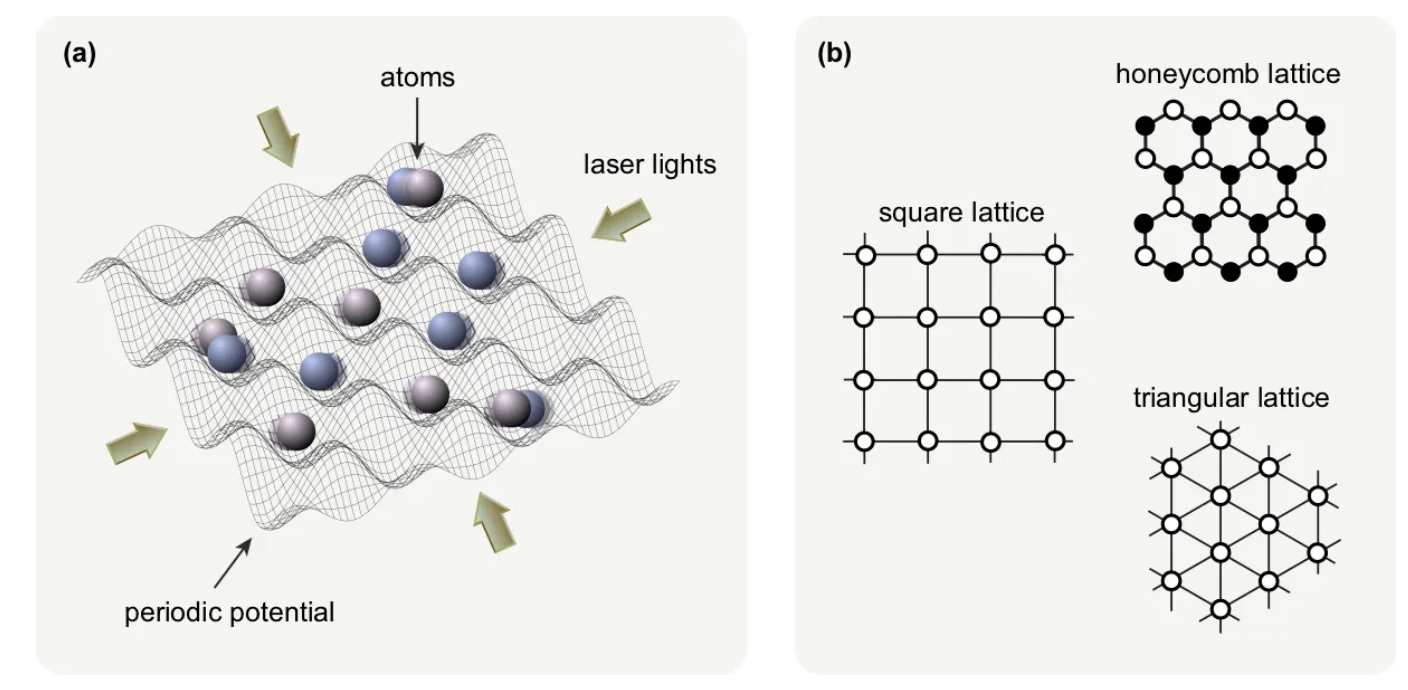
Ultracold atoms in optical lattices are a great tool to simulate quantum matter. These experimental platforms provide unprecedented control over a sizable number of atoms and are thus a crucial instrument for exploring quantum information processing at various scales. What are optical lattices exactly and how can we use them for quantum information?

Optical lattices
Optical Lattices (OL) [A1] are artificial crystals generated by pairs of counterpropagating laser beams. The nodes of the light crystal provide a position for either a single atom or group of atoms, depending on their properties. All atoms located in the lattice points must be neutrally charged to avoid light-matter interaction between lattice and particle. For studying quantum effects — which reveal themselves at very low temperatures and small scales — the atoms should be thoroughly cooled down, hence they are called ultracold atoms. The laser beams are highly tunable, which allows to create various lattice structures in different dimensions. When loaded with ultracold atoms they are an exceptional playground for realizing synthetic matter.

One very fruitful application of these setups is the quantum simulation of solid state models, which adds to gaining a deeper understanding of materials and their basic properties in addition to realistic material research. Beyond testing existing systems, within these platforms novel quantum system can be explored leading to discoveries of exotic matter and much more. In the following we explore Quantum Information Processing (QIP) exploiting OL [A2,A3].

QIP and gate based quantum computation
Before understanding what QIP is, one should recall that a classical computation is a physical process obeying the classical laws of physics while a quantum computation subject to quantum laws, particularly to the superposition principle and entanglement: The superposition principle expresses that a quantum system can be in multiple states simultaneously before it is measured. Entanglement is a non-local correlation that is due to interactions among quantum particles and is a quintessential concept in quantum information and several branches of condensed matter physics. QIP relies on encoding information into quantum states with these properties, which can be manipulated with unitary time evolutions. The input state is in a superposition of all possible basis states of the N quantum bits, or qubits, and after a measurement we will just get one of the N possible qubit states with a certain probability, which is considered the output state.

For executing a quantum computation in optical lattices, one needs a set of qubits based on two-level systems such as two internal states of the trapped atoms, which can form an array throughout the lattice and thereby shape a quantum register.

Furthermore, to achieve a programmable quantum computer based on circuit-models, the array of trapped neutral atoms must be well isolated from the environment else they are prone to decohere. To be more precise they need to be implemented in such a way that they can be operated at scales with long coherence times and the logic gates should have high fidelity with respect to the ideal target gates. To complete the construction of an OL-based quantum computer, a universal set of quantum gates must be engineered. The most natural gates in this context are single qubit and two qubit phase gates, while the latter require interactions between qubits and are thus harder to realize.

Mott insulators and their use for QIP in optical lattices
For exploring ideas how to generate single qubit gates in OL, we take a little detour into a central research topic of condensed matter, the so-called Mott Insulator (MI) [A4], a phase in which particles are unable to move due to strong repulsive interactions among them. This state was discovered by Mott and Peirls [A5] to explain why several transition-metal oxides are insulators despite indications from band theory that they seem to be metals. In these oxides the electrons feel a repulsive force when they are in the vicinity of each other and it can be described by Coulomb’s law, i.e. Coulomb repulsion. Electrons are fermions, which loosely speaking means they are the “unsocial type” of quantum particles and more rigorously it means they obey the Pauli principle that states if fermions have identical properties, they cannot occupy the same state. With properties we refer to quantum numbers used to characterize conserved quantities in the dynamics of a quantum system, e.g., in an atom they describe the movement and location of each electron. An important quantum number to label electrons is its spin (the intrinsic angular moment) which can either point up or down, which results in the label up = ↑ or down = ↓ for the spin.

The simplest model to mimic the physics of electrons in solids is the Hubbard model [A6], which has a kinetic term, describing the movement of the electrons and a Hubbard interaction approximating the Coulomb repulsion. The latter formulates: if an electron with spin-↑ and an electron with spin-↓ are located at the same spot, they repel each other (hence a fully local interaction). The model is conceptually simple, but very hard to solve!

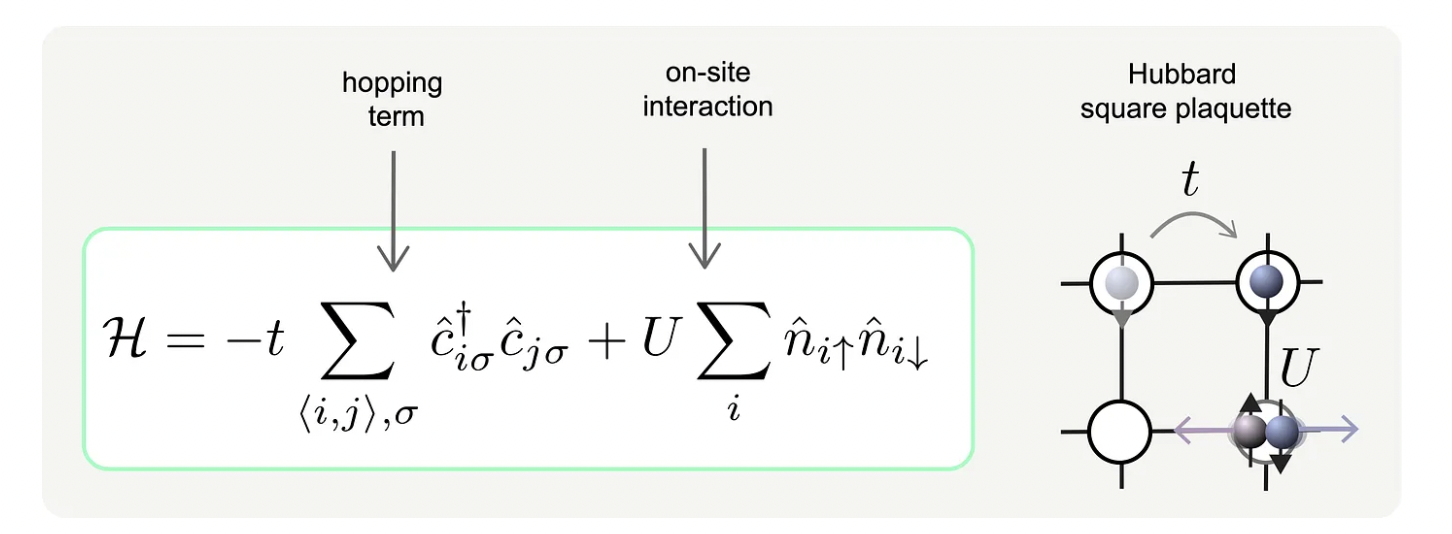
Now, imagine a lattice with N sites that is filled with N/2 spin-↑ electrons and N/2 spin-↓ electrons. When the repulsive interaction between a spin-↑ and spin-↓ electron is sufficiently strong, they want to stay away from each other. Moreover, due to their fermionic nature, electrons with an equal spin are forbidden to occupy the same position. Consequently, each lattice site is exactly filled with one electron and their movement is “frozen” i.e., the kinetic energy is completely dominated by the repulsive interaction.If, however, the kinetic energy prevails the competition, then the particles are very mobile and delocalized thus it becomes probably impossible to target and control them. For that reason Mott localization is so important for qubit production.MIs occur also in bosonic systems [A7] (bosons are the “social” particles not restrained by the Pauli principle).

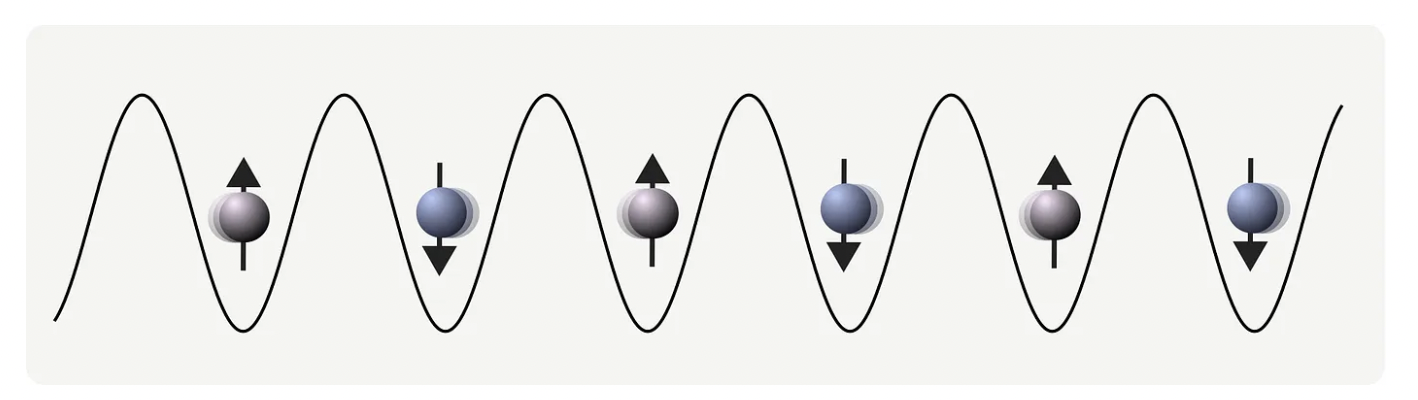
OL provide a remarkable playground to test the rich phases of different Hubbard models established to simulate the underlying physical phenomena of condensed matter systems and beyond.
To mimic the Mott physics in a cold-atom-based framework the particles must be neutral, hence they are not electrons but neutrally charged and carry a spin. When the fermions or bosons are fully Mott localized and each lattice site contains exactly one of them and thereby a qubit, it allows for easy access to single qubit gate manipulations in optical lattices, since in this set-up both internal atomic states can be trapped, which enables the storage of quantum information through a quantum register.

To execute single qubit operations, Raman transitions [A2] between two atomic states come in handy. These transitions can physically induce rotations of the qubit state on the Bloch sphere.

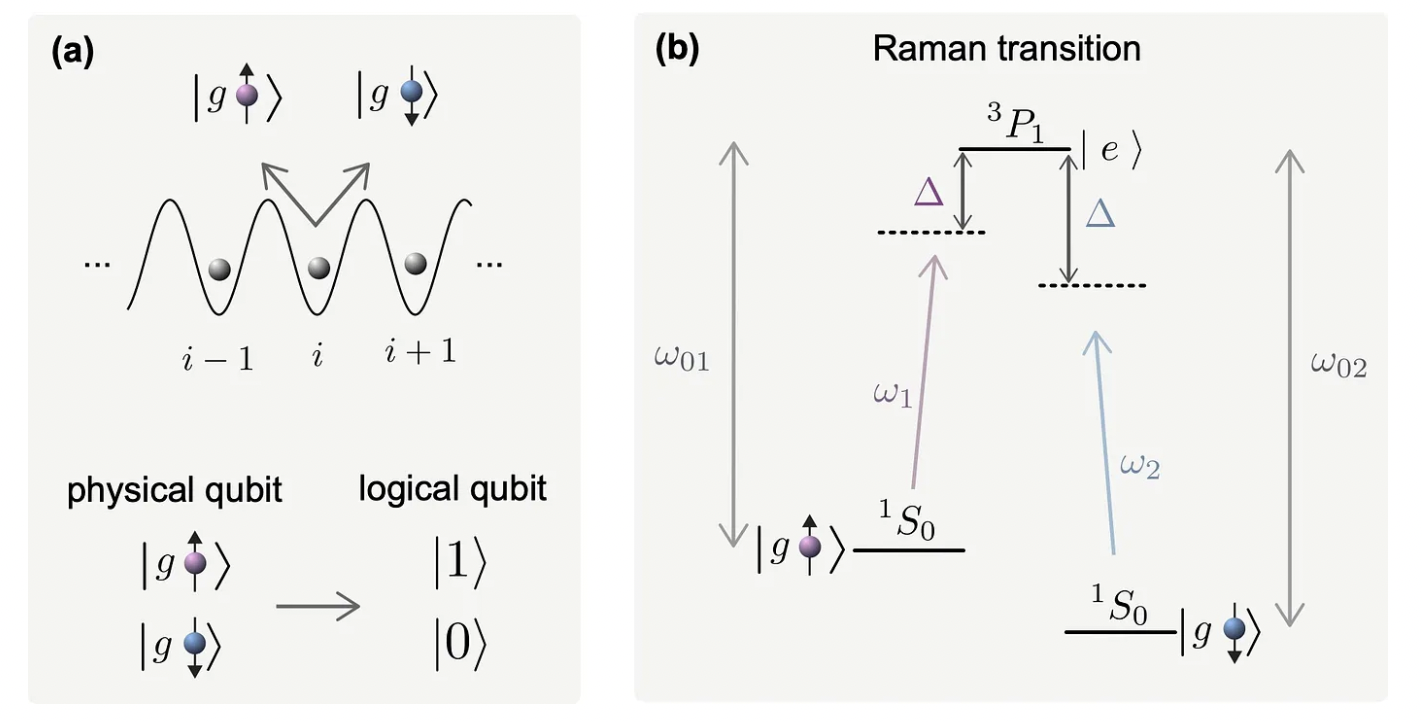
In Figure 4 (b) the Raman process [A10] for flipping the spin of the ground state is illustrated. Within this method the two ground states correspond to the two atomic resonance frequencies labelled with ω₀₁ and ω₀₂ coupled through two laser fields. This induces two photon processes in which an intermediate unpopulated excited state is occupied during the transition. With this tool not only the spin can be flipped, but depending on the choice of laser parameters, the axis and the angle of the rotation on the Bloch sphere can be tuned arbitrarily. The difficulty lies in sufficiently focusing the laser adjusted to the optical wave length separating two atoms in the lattice, but the challenge can be met with several tricks, on which we do not elaborate on.

Remarkably, qubit simulations based on MIs have already been experimentally realised and moreover they can be exploited to create multipartite entangled states. Yet, their robustness is limited to specific techniques and thus more research in MI based qubit production has to be carried out.

Two qubit phase gates
Implementing single qubit gates is already challenging, but achieving the execution of two qubit gates, e.g. due to interactions between the qubit, is even more demanding, yet there are several schemes which are able to do so. Since this article explores the possibilities of QIP within cold atoms in OL, we discuss only the most conventional concepts in this framework. It relies on the control of two-body interactions between the internal states, such as optical dipole-dipole interactions or coherent cold collisions of atoms. Let’s explore entanglement via the latter interaction.

For this we assume two atoms who are in a superposition of both internal states. The two particles are each trapped in separate potential wells and initially put very far apart to avoid any interaction between the two. Then, in order to make the two particles interact, one particle in a potential well has to be moved to the other one.

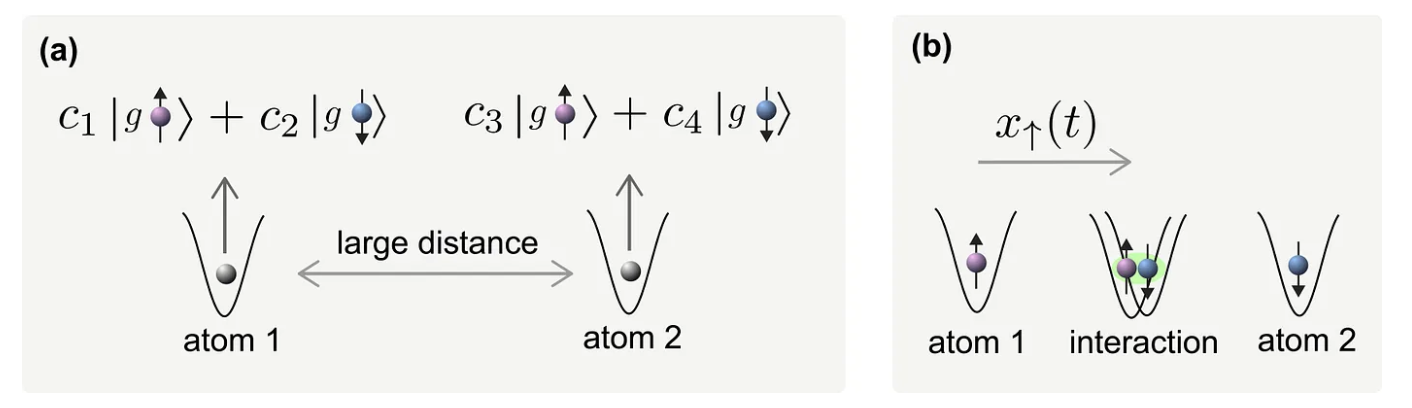
The movement must be done state selectively and for illustrative reason we say now that atom 1 on the left is in state spin-↑ and on the right atom 2 is in the spin-↓ state (see Figure 5 b). Due to the state-selective process that starts from an internal superposition and the contribution from the interaction, a phase in the wave function describing each particle is picked up. After this process the two atoms are put back to their initial position but are now entangled. If the phase coming from the collision of atom 1 and 2 is for example is π then we get the two-qubit phase gates illustrated in Figure 6 (b).

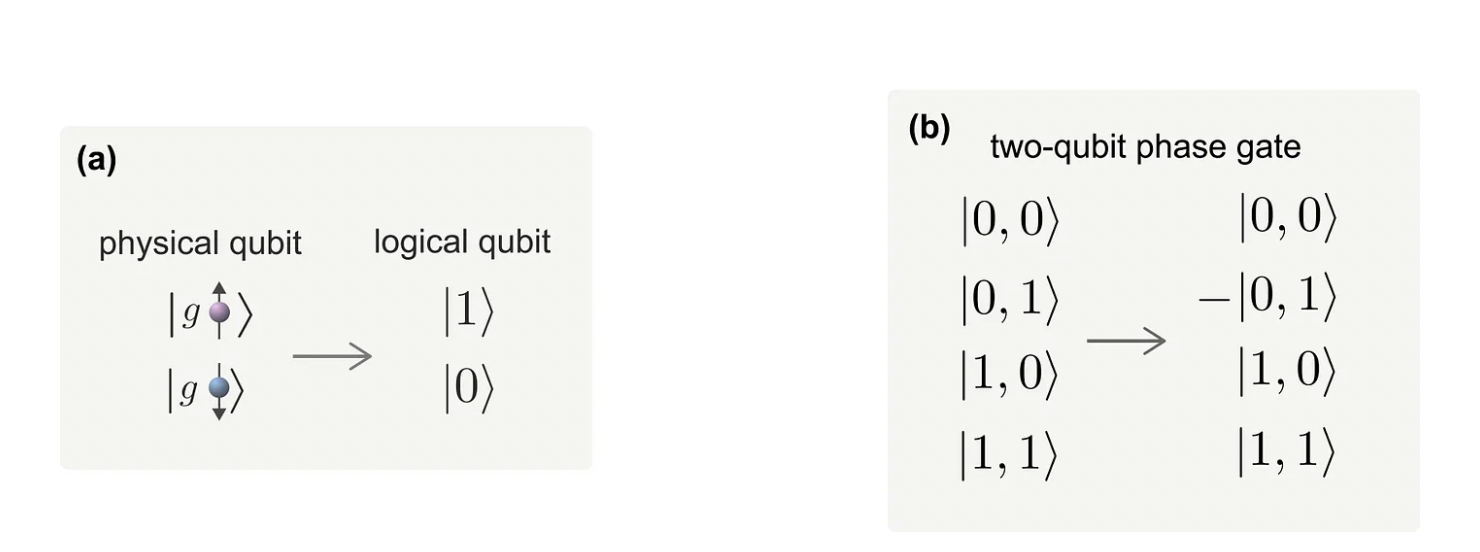
For more details we advise references [A2,A3,A8].

Scalability, Stability, and Flexibility
To conclude this introduction into QIP in cold-atom-based simulator, we emphasize that these setups are highly scalable [A9], due to the encoding of qubits in neutral atoms [A8] and the flexibility of lattice geometries that can be created. Atomic qubits can be implemented in any type of array created with laser lights, which ranges from one-dimensional to three-dimensional lattice structures. Moreover, each individual atom can be manipulated and controlled using advanced quantum gas microscopes as they experiment on in the Munich based startup planqc [W1].

‍
Owing to progress in excited Rydberg state and precise control on lasers, fast two qubit gates are enabled. Another great feature of these setup is that they promise long coherence times thanks to sufficient protection from the environment provided for example by the trapping potentials.

At ColibrITD

We believe that exploiting Quantum Information Processing in different technologies is crucial for advancing in the industrial quantum revolution. Optical-lattice-based quantum computers promise a fast way to scalable quantum computers and lead us closer to quantum advantage.

‍
Each customer’s use case demands different devices to obtain the optimal solution and we aim to understand the underlying mechanisms of each quantum hardware.

References

[A1] M. Greiner, S. Foelling, Optical Lattices
Nature Volume 453, pages 736–738 (2008)

[A2] D. Jacksch, Optical lattices, ultracold atoms and quantum information processing
Contemporary Physics Volume 45, 2004 — Issue 5

[A3] A.H. Homid, Efficient quantum gates and algorithms in an engineered optical lattice
Scientific Reports Volume 11, Article number: 15402 (2021)

[A4] N.F. Mott, The Basis of the Electron Theory of Metals, with Special Reference to the Transition Metals
Proc. Phys. Soc. A 62 416 (1949)

[A5] N.F. Mott, R. Peierls, Discussion of the paper by de Boer and Verwey
Proceedings of the Physical Society. 49 (4S): 72 (1937)

[A6] Hubbard, Electron correlations in narrow energy bands
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 276 (1365): 238–257 (1963)

[A7] D. Jacksch, Cold Bosonic Atoms in Optical Lattices
Phys. Rev. Lett. 81, 3108 (1998)

[A8] T.M. Graham et al., Multi-qubit entanglement and algorithms on a neutral-atom quantum computer
Nature Volume 604, pages 457–462 (2022)

[A9] A. J. Park et al., Cavity-Enhanced Optical Lattices for Scaling Neutral Atom Quantum Technologies to Higher Qubit Numbers
PRX Quantum 3, 030314 (2022)

[A10] D. Tusi et al. Flavour-selective localization in interacting lattice fermions
Nature Physics Volume 18, pages 1201–1205 (2022)

[W1] https://planqc.eu

‍