Interpretations of quantum mechanics

In quantum mechanics, the state of a particle can be determined through Schrödinger's Equation, representing an analogous to the well-known Newton's second law [1]. But, while from the classical counterpart, a deterministic expression for the position of the particle as a function of time x(t) can be deduced, in quantum mechanics, Schrödinger's equation allows us only to obtain a wave function ψ(x, t), spread-out in space, that does not give us any certain information about the position of the particle.

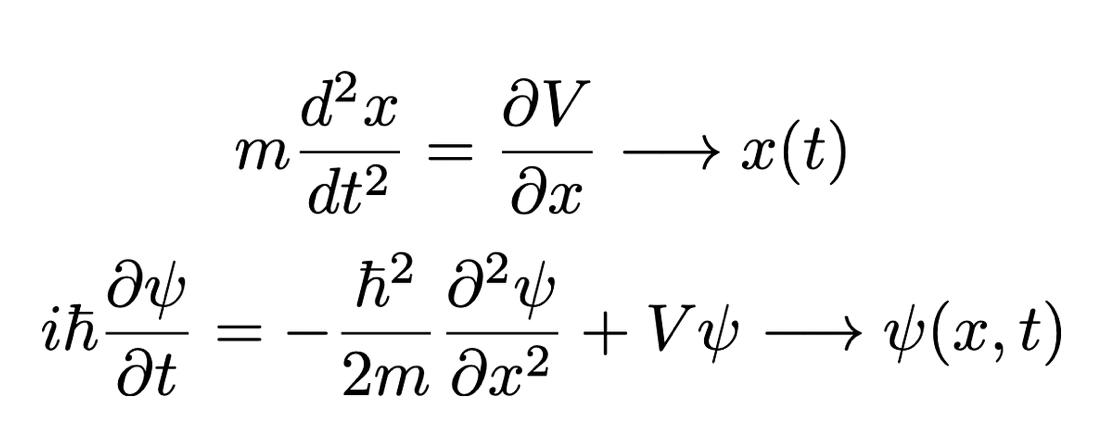
The only information we can extract about the position from this wave function comes from its squared modulus, |ψ(x, t)|², and it is probabilistic. We only know how probable is that at a fixed time, the particle will be measured in the space interval [x, x+dx] [Fig. 1 — Unobserved].

‍

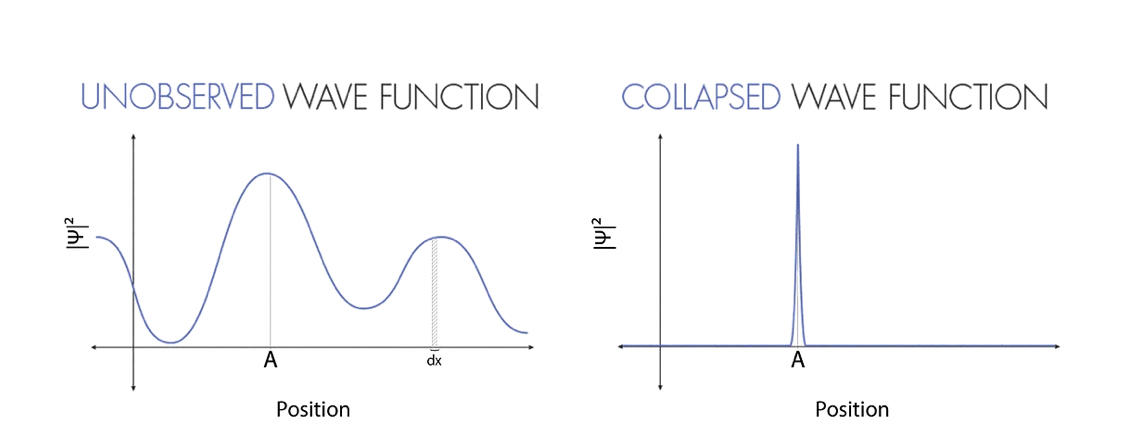
Suppose we now perform the measure, and we find out that the particle is at point A. Why were we not able to predict the position of the particle before measuring it, just like we are used to doing in classical mechanics? Is this due to a lack of information? Where was the particle before measuring its position?
There exist three different answers to the latter, that at the very early stages of Quantum Mechanics led to the division of scientists into as many schools of thought:

Orthodox The first one, known as the Orthodox position, was strongly supported by Bohr, Jordan, and Born and converged with the famous Copenhagen interpretation. According to them, the particle was not really anywhere, but it was the act of measuring that forced the particle to choose a place where to stand. Using Jordan words

"Observations not only disturb what is to be measured, [but] they produce it... The electron is forced to a decision. We compel it to assume a definite position; previously it was, in general, neither here nor there; it had not yet made its decision for a definite position." (P. Jordan) [2]

Translating this statement to the current quantum-mechanics language, the measure caused a collapse of the wave function, forcing that to peak in a very small region [Fig. 1 — Collapsed].

Realistic The particle was already at A before measuring, but we could not predict it because of a lack of information. Something is missing. In classical physics, in fact, knowing only the probabilities for a certain event to occur is the symptom of incomplete information on the system. For example, the prediction of the outcome when we toss a coin is prevented because we do not know all the parameters of this problem, such as the initial conditions for position and velocity or air pressure fluctuations. If we knew all of them, we would be able, in principle, to predict the outcome [3].

‍
One of the main sustainers of this interpretation was Albert Einstein, who was sure that one or more hidden variables existed and would have been the key to cracking this puzzle, allowing us to solve quantum mechanics equations deterministically.
In his book, A. Pais recalled one of the most crucial concepts Einstein used to explain his point of view:

“We often discussed his notions on objective reality. I recall that during one walk Einstein suddenly stopped, turned to me and asked whether I really believed that the moon exists only when I look at it.” (A. Pais) [4]

To the realist, nature was deterministic, and this indeterminacy was just a reflection of our ignorance.

Agnostic The agnostic position is based on a rejection of to answer. According to Pauli, it did not make sense to make assertions about the status of particle before the measure since the only way of stating the correctness of your assertion was to conduct a measurement. According to him, the whole subject was just metaphysics, and in his correspondence with his friend Born, he tried to convince him to give up this useless debate:

“One should no more rack one’s brain about the problem of whether something one cannot know anything about exists all the same, than about the ancient question of how many angels are able to sit on the point of a needle. But it seems to me that Einstein’s questions are ultimately always of this kind.” (W. Pauli, 1954) [5]

For several years this position was a parachute for many physicists, they started by enunciating the orthodox interpretation, but they switched to the agnostic one to quickly close the discussion [1].

Solvay congresses

The Solvay congresses on physics are invite-only scientific meetings taking place in Belgium about every 3 years since 1911. Each conference is focused on a highly topical topic of physics, and, as can be easily imagined, the first meetings were about quantum mechanics. In particular, the fifth, held in 1927, was on electrons and photons and focused on the recent rapid advances in quantum theory.

‍
The exponents of the different schools of thought were present [Fig.2], and the idea was indeed to solidify the principles of the Copenhagen interpretation, reaching the common conclusion that unknown or uncertain characteristics of measurements could not be attributed to lack of knowledge or understanding, but were fundamental and permanently inaccessible. Nevertheless, Einstein insisted on his position, which led to a strong debate between Bohr and Einstein on the meaning of quantum theory. The debate gently raged during nights and days through the fifth congress and was renewed three years later at the 1930 congress. Einstein spent days trying to conceive thought experiments without errors, with the aim to put Bohr into a corner from which he could not escape, proving the inconsistency of the theory. Einstein’s Gedankenexperiment used electrons passing through slits, diffracting as required by Schrödinger’s theory, but being classically measurements. He presented a thought experiment to Bohr, who returned shortly after with his answer, only to be confronted by yet another clever device of Einstein’s clever imagination that would force Bohr to retreat again. Anyway, Bohr was always able to find a reason why the tricky paradox Einstein came up with started indeed from wrong hypotheses [6].

Einstein was not the only disappointed scientist at the congress, and after the end of it, he and Schrödinger exchanged many letters complaining to each other about the increasing spread of statistic interpretation of quantum mechanics among scientists. Consequently, the last steps of the debate were carried out not at the Solvay Congress but directly in the Physical Review journal, where Einstein, Rosen, and Podolsky published the paper containing Einstein's punch line in this battle, the EPR paradox [7].

Einstein-Podolsky-Rosen paradox — 1935

‍
The Gedankenexperiment involves a pair of particles prepared — in what later authors would refer to as — an entangled state. Here, we are not going to present the original version, which was originally based on measures of position and momentum [8]; but instead, Bohm's simplified version of the paradox was elaborated on and published by Einstein, Podolsky, and Rosen five years after the sixth Solvay conference. Let us consider the decay of a muon π⁰ at rest in an electron e⁻ and a positron e⁺, i.e. π⁰ → e⁻ + e⁺ [Fig.3].

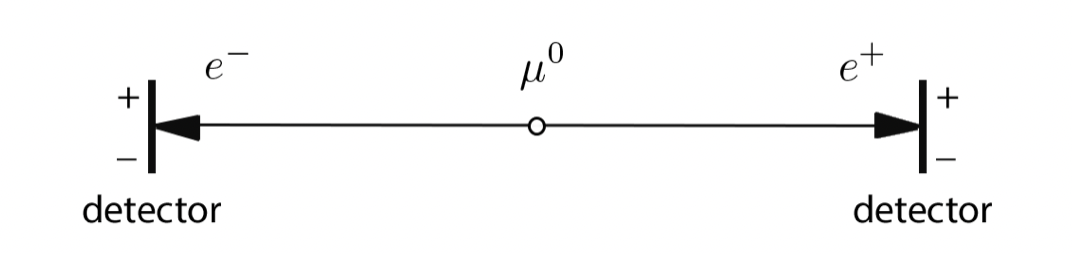
According to the principle of conservation of angular momentum, we can affirm that electron and positron are in the singlet state, i.e. (|↑₋↓₊⟩-|↓₋↑₊⟩)/√2. They have for sure opposite spins, but you cannot tell which one between the electron and the positron will have spin up or down; all you can tell is that the two measures are correlated, which means that if the electron has spin up, the positron will be found in spin down and vice-versa.

‍
It is now time to push this thought experiment a bit further. Since the muon was at rest, after its decay, the electron and the positron will fly apart from each other. What is crucial is that even if they fly 20 lightyears apart from each other, by measuring the spin-state of one of them, we will immediately know the state of the other. How do we reconcile the fact that the electron knows that the spin of positron has been measured, even though they are separated by lightyears of space and far too little time has passed for information to have traveled to it according to the rules of special relativity?

‍
According to Einstein, this peculiar behavior would be compatible only with a realist viewpoint: for the realistic school of thought, there is nothing weird, the angular momentum of the electron was down (or up), and the one of the positron was up (down) since the decay process happened. On the other hand, in the orthodox interpretation, neither the particle had spin up or down until the act of the measure forced it to choose; the measurement of the electron spin not only makes the electron wave function collapse but produces the collapse of the positron 20 lightyears away. For Einstein, Podolsky, and Rosen, this would lead to an infringement of the principle of locality: the two particles would be able to communicate faster than the speed of light.

‍
Their deduction is simple: quantum mechanics theory is correct but incomplete, and only the realistic point-of-view is acceptable. The wave function is part of the story, but it is not the whole story; some other quantity is needed in order to fully characterise the state of the system. They thought this paradox was the long-awaited check-mate, and indeed the pieces on the board remained still for almost thirty years.

‍
Unfortunately, Einstein did not live enough to see that not only the EPR paradox does not prove that quantum mechanics is incomplete, but also that, ironically, his paradox was a perfect starting point to show that statistical interpretation is indeed correct.

Bell's inequality — 1964 [9]
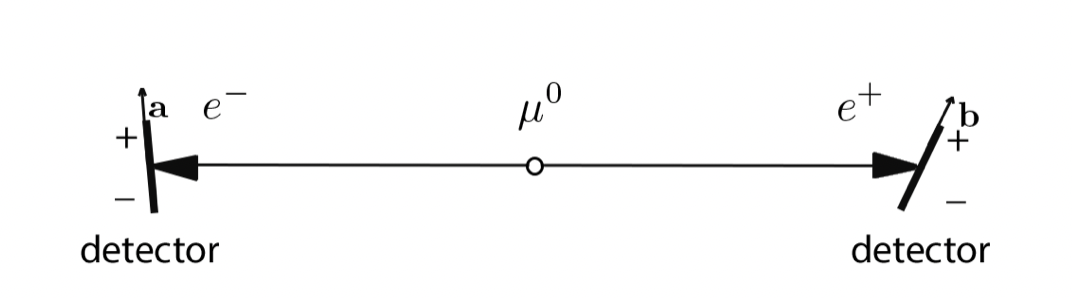
It is time to imagine the existence of this controversial hidden variable λ, which is supposed to complete the theory and save us from the intrinsic statistical nature of quantum mechanics. Bell considered a generalization of the EPR/Bohm experiment in which the electron and positron detectors are not oriented along the same direction but are instead allowed to rotate independently. The electron spin is measured along the direction of a unit vector a, while the positron one is along b [Fig.4].

The values ±1 are registered for spin up and down, respectively. The key to Bell's idea is to consider three different reciprocal orientations of the detectors, i.e. three different unit vectors a, b, and c, and to calculate the average of the product of the two spins. In a generic configuration, the value of the average can be determined as P(a, b)= -a⋅b, with for a=b, the EPR/Bohm configuration is retrieved. According to the idea of the existence of a hidden variable λ, there must exist some functions A(a, λ) and B(a, λ), taking values ±1, which gives us the exact result of an electron and a positron measurement, respectively. These two functions must be of course, perfectly anti-correlated when the two detectors are aligned, i.e. A(a, λ) = -B(a, λ) for any value of the hidden variable λ. Exploiting this property and [A(a, λ)]²=[B(a, λ)]²= 1, we manage to calculate the difference of probabilities P(a, b)-P(a, c) for any orientation of the unit vector a, b and c, obtaining

P(a, b)-P(a, c) = -∫ρ(λ)[1 - A(a, λ)A(b, λ)]A(a, λ)A(b, λ)dλ,

Where ρ(λ) is a probability density.
Since |A(a, λ)A(b, λ)| ≤ 1 and ρ(λ)[1 — A(a, λ)A(b, λ)] ≥ 0, we obtain an upper bound for the difference as follows

|P(a, b)-P(a, c)| ≤ 1 - P(c, b).

This is the famous Bell inequality. It is now time to explicitly calculate these probabilities considering a specific configuration. To simplify, we suppose that three vectors lie in a plane and that c makes a 45 degrees angle with a and b; in this case, P(a, c) = P(b, c) = -0.707, while, being a and b orthogonal, P(a, b) = 0, leading to an evident violation of Bell's inequality:

0.707 ≰ 1 – 0.707.

This inequality demonstrates that it makes an observable difference whether the particle has a precise spin before the measurement or not.

‍
Moreover, Bell's contribution to the EPR paradox leads toward a much deeper consequence than what Einstein thought: if Einstein, Rosen, and Podolsky are right, quantum mechanics is not just incomplete; it must be wrong [1].

‍
Right after Bell's result became known, many efforts in order to check if any experimental record against locality existed, but unfortunately, it was not the case. It was necessary to wait until 1982 when the work of Aspect, Grangier, and Roger came out [10]. The experimental evidence confirmed that no local hidden variable can exist and that non-local phenomena do exist in nature. Of course, the possibility of the existence of non-local hidden variables is still available, or other exotic theories such as the 'Many Worlds' interpretation [11, 12] but none of those have really been accepted by the scientific community.

‍
Anyway, it is important to notice that this superluminal communication between particles breaks the locality, but it does not imply a causal influence. In Bell's experiment, the measurement of the electron does influence the measure of the positron spin, but it does not cause it. There is no way that the person monitoring the electron detector could use the outcomes to send a signal to the person in charge of positron spin measurements. The two lists of data considered separately are completely random; it is only by comparing them that we can highlight the correlation.

At ColibrITD

At ColibrITD, we believe that understanding the interpretation of quantum mechanics deeply is essential to have a solid background in order to move forward. Mastering these counterintuitive concepts, including entanglement, is the key to starting the quantum computing revolution.

References:
[1] D. J. Griffiths, Introduction to quantum mechanics, Cambridge university press (1995).
[2] M. Jammer, The philosophy of Quantum Mechanics: The interpretations of Quantum Mechanics in historical perspective, New York, John Wiley and Sons (1974).
[3] Lecture on the statistical interpretation.
[4] A. Pais, Rev. Mod. Phys. 51, 863 (1979).
[5] Born-Einstein Letters, 1916–1955, Friendship, Politics and Physics in Uncertain Times.
[6] The Solvay Debates: Einstein versus Bohr | Galileo Unbound.
[7] A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47, 777 (1935).
[8] J. J. Sakurai and J. Napolitano, Modern Quantum Mechanics, Cambridge University Press (2017).
[9] J. S. Bell, Phys. Phys. Fiz. 1, 195 (1964).
[10] A. Aspect, P. Grangier and G. Roger, Phys. Rev. Lett. 49, 91 (1982).
[11] C. Rovelli, Helgoland (2020).
[12] Many worlds interpretation, Wikipedia (2022).