Freedom for Schrödinger's cat

As soon as quantum mechanics is mentioned, in order to astonish the interlocutors a subject is usually popped-up: the very famous Schrödinger’s cat paradox. Many use this paradox to share in a popular and easy fashion the magic of quantum mechanics, trying to give a macroscopic example of how this theory is supposed to turn upside down our way to perceive reality. Anyway, things are much different: the meaning of this Gedankenexperiment and the reason why it has been conceived in the first place are diametrically opposed. In fact, Erwin Schrödinger enunciated this paradox with the specific — albeit vain — intention to discredit one of the most incredible and counterintuitive property of quantum mechanics: the superposition, the ability of quantum system to be in multiple states at the same time until measured [1]. This feature, included in the Copenhagen interpretation — extensively treated in one of my Medium articles — was never digested by Schrödinger and Einstein. Until the end, they tried to show the incompleteness of this theory by devising increasingly complex thought experiments.It was indeed with the aim of highlighting the shortcomings of the Copenhagen interpretation and remarking the problems associated with measurement, that Schrödinger’s cat was born (and dead).

Interpretations of quantum mechanics (Medium article).

Through this article, we will virtually fight for animal rights, by trying to understand why this thought experiment may not really lead to a paradox, trying to finally set Schrödinger's cat free.
‍

Let us start from the very first formulation of this paradox, for which no animals were harmed in the making. In a letter dated August 1935, it was Albert Einstein to propose such a paradox: with the scope of exaggerating the oddness of the superposition property, he imagined a metastable gunpowder barrel, ready to explode at the slightest spark, within which a radiative atom of half-period one year was placed [2]. This physical situation implies that the gunpowder will almost certainly spontaneously explode over a one-year period, and the superposition condition of the atom entails that the moment when it blows up is at an unknown random time. Moreover, since the explosion is very fast, it can be assumed that the powder at any time is either stable gunpowder or exploded gunpowder. According to Einstein, if one assumes that the usual rules of quantum dynamics are valid up to the macroscopic level, then the existence of this quantum interference at the microscopic level necessarily implies that the same phenomenon should occur between distinguishable macroscopic states [3]. This means that Schrödinger's equation would have predicted the state of the barrel being in a superposition of two classically opposite states, stable and exploded gunpowder, before the decay event. However, he believed the reality was that the actual state of the material is perfectly determined and that the description was incomplete [4].
‍

It is in Schrödinger's answer, written later the same month, that we finally have the novel twist and the opportunity to meet the unlucky cat: the barrel is replaced by the animal, which a device — created out of a radioactive substance, a hammer and small flask of hydrocyanic acid — places in a superposition of dead and alive states. We use in the following the physicist’s original words [5]— for the sake of clarity, translated in English:

One can even set up quite ridiculous cases. A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny bit of radioactive substance, so small, that perhaps in the course of the hour one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube discharges and through a relay releases a hammer that shatters a small flask of hydrocyanic acid. If one has left this entire system to itself for an hour, one would say that the cat still lives if meanwhile no atom has decayed. The first atomic decay would have poisoned it. The ψ-function of the entire system would express this by having in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts.

It is typical of these cases that an indeterminacy originally restricted to the atomic domain becomes transformed into macroscopic indeterminacy, which can then be resolved by direct observation. That prevents us from so naïvely accepting as valid a “blurred model” for representing reality. In itself, it would not embody anything unclear or contradictory. There is a difference between a shaky or out-of-focus photograph and a snapshot of clouds and fog banks.

Both thought experiments contain in themselves also the concept of entanglement. The single atom, that can go from its excited state |e⟩ to its ground one |g⟩ by emitting a photon, is coupled to the cat (barrel). So, if the atom is "half way" between excited and ground — 1/√2 (|g⟩ + |e⟩)—, the cat (barrel) should be "half way" between |dead⟩ and |alive⟩ (|exploded⟩ and |stable⟩).

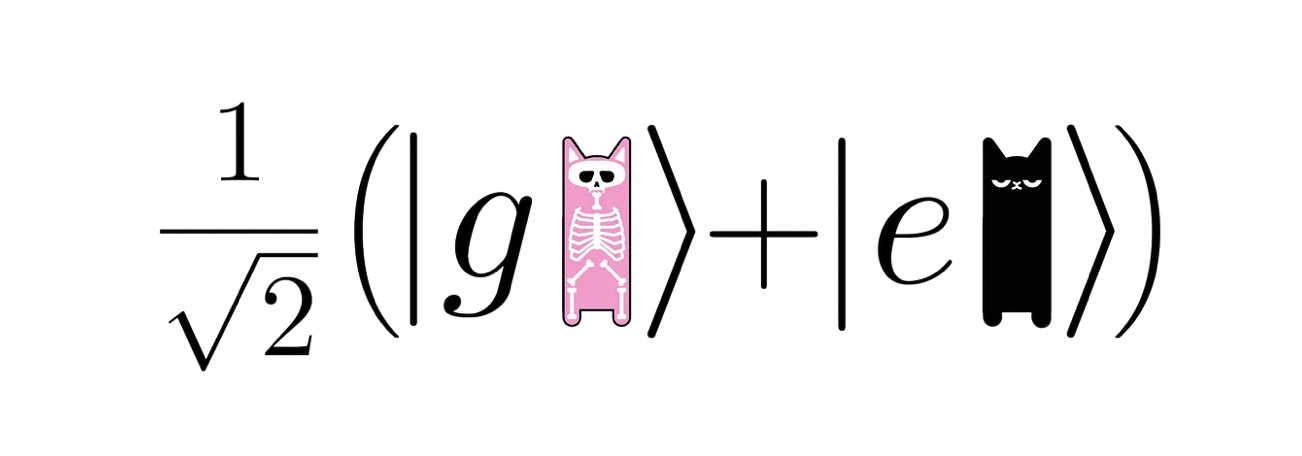
According to Schrödinger, in a weird world ruled by Copenhagen's interpretation laws, until an observer opened the box, the cat would stay in a linear superposition of dead and alive, and it would be the act of measuring to force the system to collapse and so, potentially, to kill the cat. As can be understood from the few lines above, Schrödinger himself never thought that his cat could have been simultaneously dead or alive, but he rather precisely modified Einstein's experiment to show his agreement on the wrongness of the probabilistic interpretation of quantum mechanics.

It is worth of notice that, as soon as the cat itself is assumed being a conscious observer, capable to perform itself a measurement of its surrounding environment, the paradox is broken. It is only when we consider that the cat has no consciousness at all, assuming it to represents no more than a barrel of gunpowder, that the paradox comes out. This means the experiments conceived by Einstein and Schrödinger are equivalent: going from a barrel of gunpowder to Schrödinger’s cat does not add anything — except clarity and the dramatic feature of a living body. In order to add a conscious layer to the experiment, a human being is needed in the chain (or inside the box, instead of the cat). Such a version exists and is known by the name of Wigner’s friend’s variant [6], from the name of the nobel prize Eugene Paul Wigner who first conceived the thought experiment in 1961.
Anyway, Einstein was astonished by the brilliant substitution Schrödinger performed and from the additional clarity this was conferring to the paradox enunciation. That is why, in the early September of the same year, Einstein replied [7]

“Your cat shows that we are in complete agreement. A ψ-function that contains the living as well as the dead cat just cannot be taken as a description of the real state of affairs.”

Since that very moment, also Einstein will always place a cat close to his gunpowder barrel.
A few months after this letter, Schrödinger’s today-famous cat example finally appeared in the magazine Die Naturwissenschaften [8]. For him, as for his friend, the absurd consequence of having a living-dead cat was the clear demonstration of a lack of information in the wave function.

By means of their speculations, Schrödinger and Einstein incidentally addressed a very fundamental problem: how can a macroscopic world emerge from the laws of quantum physics? This is the question their Gedankenexperimente should really prompt us to wonder about. The cat will either be dead or alive, the barrel would be stable or exploded, but how is this possible even though the microscopic world is not deterministic? So, how do we deal with this situation and solve the mystery of this paradox? Several solutions have been proposed to crack this paradox, including the existence of a small nonlinear term — unnoticeable for microscopic phenomena — in Schrödinger's equation, responsible of transforming the macroscopic quantum superpositions into statistical mixtures. Nevertheless, nowadays the most accredited explanation relies on the role of dissipation in giving rise to a phenomenon quantum computing researchers are terrified of: decoherence [9].

Decoherence
‍

Nowadays, quantum researchers are quite used to the concept of decoherence, currently one of the main obstacles to the breakthrough of quantum computers. What is decoherence? As the name suggests, decoherence is the loss of coherence for a system, i.e. the ability to show interference effects. The reason why coherence is so fragile is that superposition states for particles can be maintained only in the absence of interactions with the surrounding environment, being this latter guilty of triggering and forcing the quantum system to precisely take a "position" between the states. In this process, the quantum superposition is turned into a statistical mixture, for which all the information on the system can be described in classical terms, so our usual perception of the world is recovered.
As soon as it is clear how fragile a superposition state is even for a microscopic object, it becomes easy to understand that preserve coherence for a macroscopic object would be basically impossible. Each of its 10²³ particles should be protected from any interactions with the environment, e.g. collision with a lot of uncontrolled particles such as air molecules. Indeed, each time a collision would occur, the environment's particle would take away some information about the object properties, such as the position. Technically speaking, what we are dealing with is a growing entanglement between those particles and the macroscopic object [3], which would be at the end coupled to a large reservoir of microscopic variables inducing a fast dissipation of any track of its macroscopic coherences [10]. We can consider the decoherence as a measurement process: it is not the presence of a conscious observer to cause the collapse of the wave function.
‍

Furthermore, quantum coherence decay time would be given by the energy dissipation time divided by a dimensionless number measuring the ‘‘separation’’ between the two parts. The statement that these two states are macroscopically separated implies that this dimensionless quantity is an extremely large number. Going back to our macroscopic four-legged friend, the process of decoherence is then almost instantaneous, so that the state of the cat is well determined even before someone decides to open the box in which it has been unjustly confined.
‍

To remove all doubts about the impossibility to observe an interference phenomenon for a macroscopic object even in the forthcoming years, it makes sense to imagine an ideal situation in which we manage to completely isolate our macroscopic object from the environment. If we suppose that no interactions with its surrounding can occur, we can agree that, in some ultimate sense, the object would be still described by the laws of quantum mechanics. From a mathematical point of view, its wave functions would be described by an extremely complicated object, composite of all the wave function of its 10²³ constituent particles: somewhere in the statistics of large numbers, macroscopic linear combinations become anyway extremely improbable — i.e. impossible—[11].
As a conclusion, such a superposition state, known in literature also as "Schrödinger's cat state", only exists for sufficiently small objects.

Cat states and qubit states
Even though the idea of creating a macroscopic superposition is hopeless, it has been experimentally proven that mesoscopic superpositions can exist [3]. Nowadays, creating a cat states in the lab is a routine task. This is usually accomplished by using microwave oscillators — either in the form of superconducting cavities or resonators on a chip — coupled to devices containing Josephson junctions [12]. More than two decades ago, it has been pointed out that that these states can be used to encode a qubit of information in an oscillator [13]. For example, a cat state using even and odd coherent states of a single optical mode is the base of the so-called cat qubits[14], which seem to be promising for hardware-efficient universal quantum computing. As a matter of fact, these cat-state qubits are noise biased [15] and the qubits based on this technology experience only bit-flip noise, while the phase-flip errors are exponentially suppressed. As a consequence, additional layers of error correction can focus only on the bit-flip error — as explored in my last medium article— so that the number of building blocks can be significantly reduced [14].

Can we really deal with bit flip? (Medium article)

At ColibrITD

At ColibrITD our aim is to choose the best hardware to tackle our customers’ use case. That requires familiarity with the challenges and difficulties arising while building such a powerful technology.

References
[1] Wikipedia contributors, Young’s interference experiment, Wikipedia — The Free Encyclopedia (2023).
[2] Vincent Bontems, Zoologie quantique : le chat des possibles (2018).
[3] L. Davidovich, M. Brune, J.-M. Raimond and S. Haroche, Mesoscopic quantum coherences in cavity QED: preparation and decoherence monitoring schemes, Phys. Rev. A., 53, 1295–1309 (1996).
[4] Michael Steiner, notes.
[5] J. D. Trimmer, The Present Situation in Quantum Mechanics: A Translation of Schrödinger’s “Cat Paradox” Paper, Proceedings of the American Philosophical Society, 124, 323 (1980).
[6] Wikipedia contributors, Wigner’s friend, Wikipedia — The Free Encyclopedia (2023).
[7] A. Fine, The Shaky Game: Einstein, Realism, and the Quantum TheoryUniversity of Chicago Press, Chicago (1986).
[8] Schrödinger, Erwin (1935). “Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics)”. Naturwissenschaften.
[9] Imperial College London, Schrödinger lecture 2014: Professor Serge Haroche — Shedding new light on Schrödinger’s cat, YouTube (2014).
[10] M. Brune, E. Hagley, J. Dreyer, X. Maître, A. Maali, C. Wunderlich, J. M. Raimond, and S. Haroche, Observing the Progressive Decoherence of the “Meter” in a Quantum Measurement, 77, 4890 (1996).
[11] D. J. Griffiths, Introduction to quantum mechanics, Cambridge university press (1995).
[12] P. Arrangoiz-Arriola and E. Campbell, Designing a fault-tolerant quantum computer based on Schrödinger-cat qubits, AWS Quantum Technologies Blog,(2021).
[13] P. T. Cochrane, G. J. Milburn, and W. J. Munro, Macroscopically distinct quantum-superposition states as a bosonic code for amplitude damping, Phys. Rev. A 59, 2631 (1999).
[14] Using ‘cat states’ to realize fault-tolerant quantum computers, Phys.org (2022).
[15] Y.-H. Chen, R. Stassi, W. Qin, A. Miranowicz, and F. Nori, Fault-tolerant multiqubit geometric entangling gates using photonic cat-state qubits, arXiv:2109.04643v5 (2022).

‍

‍